В повседневной жизни, мы большей частью стараемся иметь дело с
локально-линейными объектами Пространства-Времени, где прямая - кратчайшее
расстояние: "срезаем углы" и перебегаем дорогу на красный свет.
К сожалению, в целом Вселенная устроена весьма нелинейно - в гости к
соседу из соседнего подъезда приходится ходить через улицу, а не через пролом
в стене.
Тем не менее, идеализированные линейные (евклидовы) миры изучены и интуитивно
понятны лучше всего. Встречая нелинейность, мы прежде всего задумываемся,
нельзя ли ее как-либо "линеаризовать".
Один из способов "линеаризации" - поиск таких характеристик, которые
позволяли бы "линейно" сопоставлять нелинейные объекты сложной конфигурации.
Исторически первыми, очевидно, были меры расстояния, веса, объема и времени.
В сущности, все они были взаимозаменяемы. Расстояние могло определяться в
днях пути, время - объемом вытекшей из клепсидры воды, объем - весом сосуда.
Даже в наше время, несложно представить работу "от забора - до обеда".
Развитие технологий очень быстро добавило к списку измерение площадей и
универсальную меру для всего - деньги.
Деньги, как единая мера всех вещей, обладали тремя важными качествами:
- Измеримость. Их удобно считать.
- Аддитивность. Их можно накапливать.
- Упорядоченность. Можно указать, у кого их больше.
Идея универсальной валюты сыграла важную роль в экономике, но главный ее
триумф - все есть Энергия - случился в физике, завершившись самой знаменитой в
истории формулой Теории Относительности Эйнштейна
E = m * c^2
В поисках подходящей оценки для сообщений, Шеннон, несомненно, придерживался
той же концепции "денежного эквивалента", позволявшего бы сравнивать
разнородные тексты "по стоимости". К несчастью, он делал это в терминах
"вероятности".
В 1927 году на международном конгрессе по телефонии, Ральф Хартли выдвинул
первый формальный вариант такой оценки (R.V.L. Hartley "Transmission of
Information" BSTJ 535—563, 1928. Перевод В.В. Фурдуева).
Для того чтобы мера информации имела практическую, инженерную ценность, она
должна быть такой, чтобы информация была пропорциональна числу выборов.
Поэтому число возможных последовательностей не годится для
непосредственного использования в качестве меры информации. Однако его
можно использовать как основу для построения производной меры,
удовлетворяющей практическим требованиям. Для этого будем произвольно
считать, что количество информации пропорционально числу выборов, а
коэффициент пропорциональности выберем таким образом, чтобы равцым числам
возможных последовательностей соответствовали равные количества информации.
H = n*Log(s)
Интересно, что при обосновании своего предложения, Хартли апеллирует к
аналогии с мощностью:
Сделанное нами сводится, следовательно, к тому, что в качестве практической
меры информации мы берем логарифм числа возможных последовательностей
символов. Положение сходно с тем, которое мы встречаем при измерении
затухания, вносимого включением некоторого звена в систему телефонной
передачи. Эффект от такого включения сводится к изменению в некотором
определенном соотношении мощности, отдаваемой приемнику. Это соотношение
можно принять в качестве затухания. Однако оказывается более удобным взять
в качестве меры затухания логарифм отношения мощностей.
И, более того, будучи радиоинженером, вводит энергетический инвариант:
Это приводит нас к важному выводу, что максимальная скорость передачи
информации, возможная в системе, частотный диапазон которой ограничен
некоторой областью, пропорциональна ширине этой полосы частот. Отсюда и
следует, что общее количество информации, которое может быть передано
посредством такой системы, пропорционально произведению передаваемой полосы
частот на время, в течение которого система используется для передачи.
Произведение передаваемой полосы частот на время и есть упомянутый мною в
начале статьи количественный критерий сравнения передающих систем.
Очевидно, оценка Хартли могла послужить хорошим стартом для дальнейших
улучшений. Но она не делает различий между выборами, рассматривая пространство
состояний как полностью однородное, пренебрегая не только семантикой
сообщения, но и возможным взаимовлиянием между символами.
Шеннон вводит два существенных дополнения.
Первое из них связано с алфавитным расслоением пространства состояний.
Если Хартли, как практический инженер, интересовался прежде всего
"энергетическим" инвариантом - общим количеством информации (Quantitative
Expression for Information) для оценки физической реализуемости систем
коммуникации, то Шеннон задается вопросом о "парциальной мощности" каждой
буквы алфавита и переходит, с этой целью, от абсолютных количеств к
нормированному пространству - вероятностям.
Второе требует взаимной независимости всех выбранных расслоений.
В сумме, это означает введение многомерного пространства состояний с числом
координат (степеней свободы) равным размеру выбранного алфавита.
Следуя выбранной вероятностной модели, Шеннон отказывается от
"энергетического" инварианта Хартли и рассматривает индивидуальные вероятности
как меру неопределенности.
Возможно, под влиянием идей Н. Винера, информация - слово из словаря -
становится для него осязаемым сигналом на входе кибернетической системы
передачи данных - Ideal Repeater.
Нет изменения сигнала - нет информации. Чем меньше отклонение сигнала от
ожидаемого (в терминологии Шеннона - неопределенность), тем меньшую он несет
информацию. Радиоинженер немедленно узнает описание дифференцирующей цепочки.
Понятие "количество информации" в трактовке Шеннона вырождается в ошибку
прогноза. Или, в кибернетическом эквиваленте, во входное воздействие в системе
с единичной отрицательной обратной связью.
Впрочем, Шеннона заботит другое. Оценка Хартли была предложена для однородной
смеси равновозможных исходов. Как обобщить ее на неравновесный случай?
Шеннон начинает с расмотрения простейшего случая - бинарной смеси. Возможны
только два булевских (ему нравится это слово) исхода - TRUE или FALSE. Таких,
как выпадение одной из сторон монеты, например.
Два предельных варианта - максимальная определенность (монета фальшивая и
всегда выпадает одной стороной) и максимальная неопределенность (монета
симметрична, выпадение любой из сторон равновозможно).
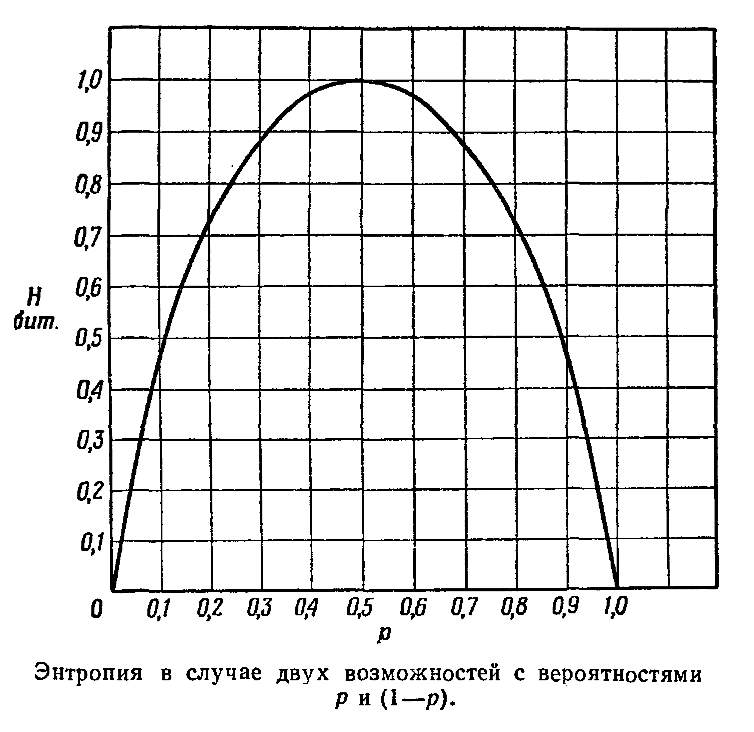 Симметрия выбора диктует симметрию количества информации.
Если исход точно известен заранее, то какой бы стороной не выпадала фальшиывя
монета: всегда аверсом или всегда реверсом, никакой новой информации при
броске мы не получаем.
И наоборот, при одинаково неизвестных исходах броска, кажется логичным
получение максимальной информации - как устранения максимальной
неопределенности.
В такой бинарной игре, определение Информации как комплемента Неопределенности
не выглядит спекулятивным, это просто единичная сумма вероятностей обоих
возможных исходов.
Теперь, когда общее поведение оценки Информации понятно, можно перейти к
многокомпонентным смесям.
В своей статье 1948 года (A mathematical theory of communication, BSTJ 27
(1948), №3, 379—423; 27 (1948), №4, 623—656) Шеннон вводит понятие
информационной энтропии. Он пишет:
Основная задача связи состоит в точном или приближенном
воспроизведении в некотором месте сообщения, выбранного для передачи
в другом месте. Часто сообщения имеют значение т. е. относятся к
некоторой системе, имеющей определенную физическую
или умозрительную сущность, или находятся в соответствии с некоторой
системой. Эти семантические аспекты связи не имеют отношения
к технической стороне вопроса.
...
Если множество возможных сообщений конечно, то число сообщений
или любую монотонную функцию от этого числа можно рассматривать
как меру информации, создаваемой выбором одного
сообщения из этого множества, в предположении, что все сообщения
равновероятны. Как было указано Хартли, наиболее естественно
выбрать логарифмическую функцию. Хотя это определение должно
быть значительно обобщено при рассмотрении влияния статистической
структуры сообщения и при наличии непрерывного множества
сообщений, будем по существу во всех случаях пользоваться
логарифмической мерой.
...
6. Выбор, неопределенность и энтропия
Дискретный источник информации был представлен как марковский процесс.
Можно ли определить величину, которая будет измерять в некотором смысле,
как много информации создается таким процессом, или, лучше, с какой
скоростью она создается? Предположим, что имеется некоторое множество
возможных событий, вероятности осуществления которых суть р1,р2,.., рN, Эти
вероятности известны, но это — все, что нам известно относительно того,
какое событие произойдет. Можно ли найти меру того, насколько велик "выбор"
из такого набора событий или сколь неопределенен для нас его исход? Если
имеется такая мера, скажем Н(р1,р2,...,рN), то разумно потребовать, чтобы
она обладала следующими свойствами:
1. H должна быть непрерывной относительно р[i].
2. Если все р[i] равны, р[i] = 1/N, то Н должна быть монотонно возрастающей
функцией от N. В случае равновероятных событий имеется больше возможностей
выбора или неопределенности, чем в случае, когда имеются разновероятные
события.
3. Если бы выбор распадался на два последовательных выбора, то первоначальная
H должна была бы быть взвешенной суммой индивидуальных значений H. Смысл этого
иллюстрируется рисунком:
Симметрия выбора диктует симметрию количества информации.
Если исход точно известен заранее, то какой бы стороной не выпадала фальшиывя
монета: всегда аверсом или всегда реверсом, никакой новой информации при
броске мы не получаем.
И наоборот, при одинаково неизвестных исходах броска, кажется логичным
получение максимальной информации - как устранения максимальной
неопределенности.
В такой бинарной игре, определение Информации как комплемента Неопределенности
не выглядит спекулятивным, это просто единичная сумма вероятностей обоих
возможных исходов.
Теперь, когда общее поведение оценки Информации понятно, можно перейти к
многокомпонентным смесям.
В своей статье 1948 года (A mathematical theory of communication, BSTJ 27
(1948), №3, 379—423; 27 (1948), №4, 623—656) Шеннон вводит понятие
информационной энтропии. Он пишет:
Основная задача связи состоит в точном или приближенном
воспроизведении в некотором месте сообщения, выбранного для передачи
в другом месте. Часто сообщения имеют значение т. е. относятся к
некоторой системе, имеющей определенную физическую
или умозрительную сущность, или находятся в соответствии с некоторой
системой. Эти семантические аспекты связи не имеют отношения
к технической стороне вопроса.
...
Если множество возможных сообщений конечно, то число сообщений
или любую монотонную функцию от этого числа можно рассматривать
как меру информации, создаваемой выбором одного
сообщения из этого множества, в предположении, что все сообщения
равновероятны. Как было указано Хартли, наиболее естественно
выбрать логарифмическую функцию. Хотя это определение должно
быть значительно обобщено при рассмотрении влияния статистической
структуры сообщения и при наличии непрерывного множества
сообщений, будем по существу во всех случаях пользоваться
логарифмической мерой.
...
6. Выбор, неопределенность и энтропия
Дискретный источник информации был представлен как марковский процесс.
Можно ли определить величину, которая будет измерять в некотором смысле,
как много информации создается таким процессом, или, лучше, с какой
скоростью она создается? Предположим, что имеется некоторое множество
возможных событий, вероятности осуществления которых суть р1,р2,.., рN, Эти
вероятности известны, но это — все, что нам известно относительно того,
какое событие произойдет. Можно ли найти меру того, насколько велик "выбор"
из такого набора событий или сколь неопределенен для нас его исход? Если
имеется такая мера, скажем Н(р1,р2,...,рN), то разумно потребовать, чтобы
она обладала следующими свойствами:
1. H должна быть непрерывной относительно р[i].
2. Если все р[i] равны, р[i] = 1/N, то Н должна быть монотонно возрастающей
функцией от N. В случае равновероятных событий имеется больше возможностей
выбора или неопределенности, чем в случае, когда имеются разновероятные
события.
3. Если бы выбор распадался на два последовательных выбора, то первоначальная
H должна была бы быть взвешенной суммой индивидуальных значений H. Смысл этого
иллюстрируется рисунком:
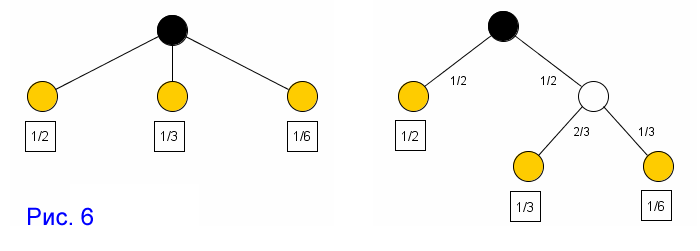 Слева имеются три возможности p1 = 1/2; р2 = 1/3; р3 = 1/6. Справа
производится выбор между двумя возможностями, причем каждая имеет вероятность
1/2, и в случае осуществления второй возможности производится еще один выбор
между двумя возможностями с вероятностями 2/3; 1/3. Окончательные результаты
имеют те же самые вероятности, как и прежде. Потребуем в этом конкретном
случае, чтобы
H(1/2,1/3,1/6) = H(1/2,1/2) + 1/2 * H(2/3,1/3) (*)
Коэффициент 1/2 является весовым множителем, введенным из-за того, что второй
выбор осуществляется только в половине всех случаев.
Комментаторы Шеннона, кажется, не обращали внимания на этот рисунок (сходный
есть и в другой статье), между тем он много дает для понимания физического
смысла информационной энтропии.
Разделим, для наглядности, систему на сумму двух подсистем, так как это
сделано для правой части уравнения энтропии.
Слева имеются три возможности p1 = 1/2; р2 = 1/3; р3 = 1/6. Справа
производится выбор между двумя возможностями, причем каждая имеет вероятность
1/2, и в случае осуществления второй возможности производится еще один выбор
между двумя возможностями с вероятностями 2/3; 1/3. Окончательные результаты
имеют те же самые вероятности, как и прежде. Потребуем в этом конкретном
случае, чтобы
H(1/2,1/3,1/6) = H(1/2,1/2) + 1/2 * H(2/3,1/3) (*)
Коэффициент 1/2 является весовым множителем, введенным из-за того, что второй
выбор осуществляется только в половине всех случаев.
Комментаторы Шеннона, кажется, не обращали внимания на этот рисунок (сходный
есть и в другой статье), между тем он много дает для понимания физического
смысла информационной энтропии.
Разделим, для наглядности, систему на сумму двух подсистем, так как это
сделано для правой части уравнения энтропии.
 Без сомнения, Шеннон трактовал эти диаграммы как вероятности переходов в
марковской цепи, но для дальнейшего изложения, удобнее рассматривать
эквивалентную дуальную цепь, где вероятности узлов заменены на потоки в
ветвях, а коэффициенты передачи ветвей исходной диаграммы Шеннона, наоборот,
отнесены к узлам.
Из сопоставления Splitted-диаграммы уравнению (*) очевидно, что потоки ветвей
суммируются в узлах (расщепляются соответственно их коэффициентам передачи), а
полный поток всей системы (полный поток вероятности) равен 1.
Диаграмма не дает верного представления об информационной цепи, поэтоиу
перейдем к схеме замешения.
Без сомнения, Шеннон трактовал эти диаграммы как вероятности переходов в
марковской цепи, но для дальнейшего изложения, удобнее рассматривать
эквивалентную дуальную цепь, где вероятности узлов заменены на потоки в
ветвях, а коэффициенты передачи ветвей исходной диаграммы Шеннона, наоборот,
отнесены к узлам.
Из сопоставления Splitted-диаграммы уравнению (*) очевидно, что потоки ветвей
суммируются в узлах (расщепляются соответственно их коэффициентам передачи), а
полный поток всей системы (полный поток вероятности) равен 1.
Диаграмма не дает верного представления об информационной цепи, поэтоиу
перейдем к схеме замешения.
|