Избыточность. Числовой пример

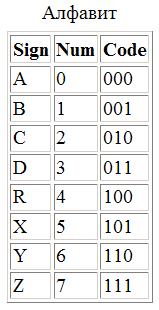
Рассмотрим простой численный пример: Алиса договаривается с Бобом об отсылке
тестового письма, которое будет состоять из единственного слова, составленного
из букв 8-символьного алфавита. Каждая буква такого алфавита может быть
закодирована не более чем тремя битами.



Кроме того, Алиса договаривается с Бобом о методе компрессии - будет
использован static Huffman.

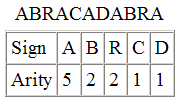
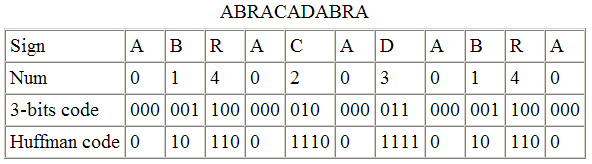
Алиса создает тестовое сообщение из пяти букв оговоренного алфавита:
"ABRACADABRA". В таблице указаны их кратности (количество вхождений каждой
буквы в текст).



Расчитаем, прежде всего, размер координатного пространства для данного сообщения,
как сумму произведений числа символов сообщения на их битовый размер. Эта
характеристика, которую будем называть битовой мощностью сообщения P имеет
смысл инварианта преобразования алфавита: при изменении размера алфавита, в
котором записано сообщение в k раз, размер сообщения соответственно
изменяется, сохраняя неизменным их произведение. Таким образом, P имеет тот же
самый смысл энергетического инварианта сигнала, что и произведение полосы
частот на длительность в аналоговых системах (Соотношение неопределенностей).

В геометрических терминах, синхронное изменение их размеров является
гиперболическим поворотом.

Сообщение "ABRACADABRA" записано 11 символами 5-ти буквенного алфавита.

В таблице показано распределение кратностей букв. Оригинальный (несжатый)
поток имеет размер 11 * 3 = 33 бита. Руководствуясь этой таблицей, Алиса
конструирует для сообщения "ABRACADABRA" дерево Хаффмана.



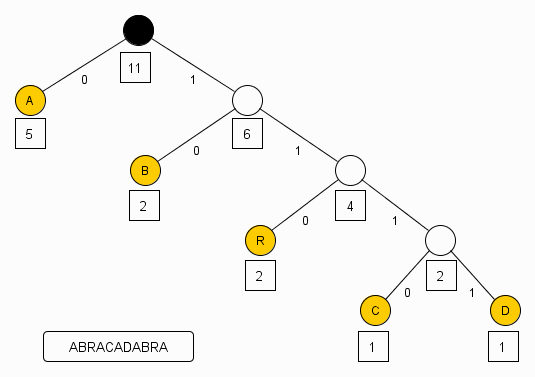И кодирует каждую букву сообщения соответственно ее расположению в
терминальных узлах дерева



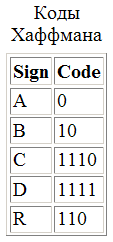Получая, в результате, сжатый поток символов



Окончательно, этот поток символов может быть снова разбит на трехсимвольные
комбинации и передан по линии связи как набор символов из заданного
8-символьного алфавита.



Заметим, что имеется некоторый произвол в выборе последнего бита, так как
размер сжатого потока (23 бита) не кратен 3 и последний 24-ый бит не
определен. Договоримся, что "хвостовые" биты всегда сбрасываются в нуль. Для
декодера значение этих битов неважно, так как декодирование закончится по
исчерпанию сжатого потока.



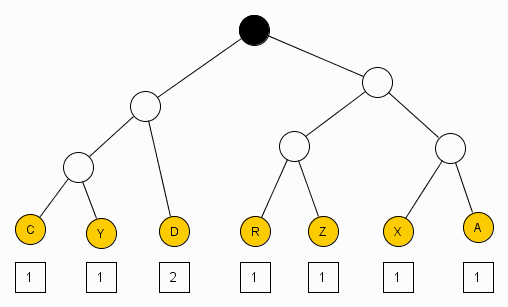Как видно из рисунка, на котором показано дерево Хаффмана для сжатого потока,
оно практически сбалансировано (и, во всяком случае, не может быть
сбалансировано лучше), что исключает возможность дальнейшего сжатия данным
методом в заданном алфавите. Разумеется, это не означает, что текст будет
несжимаем другим методом или в другом алфавите. Разница размеров исходного (33
бита) и сжатого (24 бита) потоков составляет 9 бит (фактически, 10 - без
округления) и, как объясняется в книжках, за счет "устранения избыточности".

Следует оговориться, что размер координатного пространства является инвариантом
только в случае независимых координат, иначе сообщение может быть вложено в
пространство меньшей размерности.

Тем не менее, "оптимальное кодирование" неравномерными разделяемыми кодами
неоптимально в любом случае - некоторые состояния обязаны быть запрещенными
(иначе коды перестанут быть разделяемыми) и, в силу неравенства
Крафта-Макмиллана, предельное сжатие достигается только в случае, когда код
перестает быть неравномерным.

Можно еще сравнить полученные оценки с классическими энтропийными (опять-таки,
в предположении независимости всех символов).

Шенноновская энтропия сообщения "ABRACADABRA" H = 2.04037 и его избыточность
для 8-символьного алфавита R = 1 - 2.04037 / 3 = 0.320.

Шенноновская энтропия сообщения "CYDRZXDA" H = 2.75 и его избыточность для
8-символьного алфавита R = 1 - 2.75 / 3 = 0.083.

На практике, результат может быть значительно хуже, так как необходимость
передать служебную информацию для декодера (таблицы частот или структуру
кодового дерева итп) для короткого сообщения сведет на нет весь выигрыш от
компрессии.

Сжатие коротких сообщений (таких, как SMS, например), требует перенесения
акцента с кодирования в канале передачи на конструирование разделяемой модели
(a la T9).

Понятие "избыточность", относится только к способу кодирования (выбранному
алфавиту) и никак не связано с информационным содержанием (размером
пространства состояний) самого сообщения.

Оперируя понятием "дерево выбора", можно сказать, что шенноновская энтропия
задает расстояние от корня дерева до выбранного узла, а "избыточность"
характеризует "разность хода" от корня до выбранного узла на полностью
симметричном (равновероятном) дереве и на реально существуюшем дереве.

Использование термина "избыточность" для оценки информационного
содержания сообщения - признак технической некомпетентности. Вычисление
"избыточности" сообщения записанного в двух разных алфавитах
равнозначно вычислению разности частот несущих для радиопередачи, ведущейся
одновременно в двух разных диапазонах, например, на коротких и длинных
волнах. Эта разность, разумеется, существует и может быть вычислена, но не
имеет ни малейшего отношения к характеристикам самой радиопередачи.

Ранее была использована аналогия с Фурье-преобразованием аналогового сигнала
(длительность - ширина спектра). Выясним, насколько она оправдана.

Представим текстовое сообщение в виде эквивалентной ортогональной матрицы
инциденций, строки которой соответствуют позиции символа в сообщении, а
столбцы - позиции символа в алфавите.

Для сообщения "ABRACADABRA" матрица будет состоять из 11 строк (по числу букв
в сообщении) и 8 столбцов (по числу символов алфавита).



Последние три столбца в данном случае нулевые, но тем не менее их необходимо
учитывать, так как в общем случае произвольного сообщения, могут быть
использованы все буквы заданного алфавита.



Матрица для сжатого сообщения выглядит аналогично. Если обозначить матрицу
исходного текста - x, матрицу сжатого текста - y и операцию компрессии - T, то
можно записать формальное равенство:



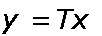Рассматривая кодовые символы как независимые векторы в полном кодовом
пространстве, можно считать, что они направлены по осям N-мерного эллипсоида
и совпадают с его положительными полуосями.

Схематично, это показано на рисунке, где кодовым символам соответствуют
векторы на плоскости.



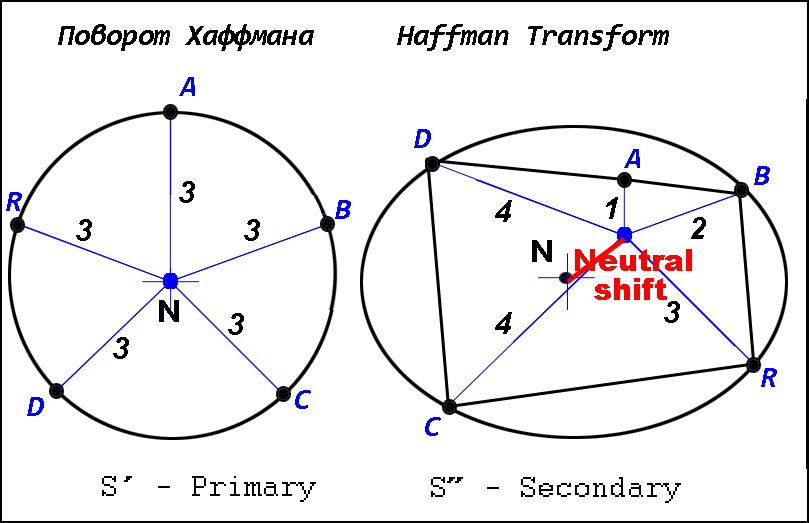При переходе от системы равномерных кодов S' к неравномерной S'' с использованием
оптимального кодирования, сдвиг и поворот каждого вектора задается
преобразованием Хаффмана, а при обратном переходе, от неравномерных кодов к
равномерным - преобразованием Тансталла.

Рассматривая отдельный кодовый символ на фазовой плоскости (w,q), где

   w -  битовая ширина кода,
а
   q -  кратность кода в сообщении,

можно трактовать изменение его битовой ширины как поворот и масштабирование,
причем знак и величина изменения зависят от отклонения исходного вектора от
условного среднего (алфавитной нейтрали).

Инвариантом этого преобразования является размер координатного пространства
системы (число степеней свободы). Чем больше кратность отдельных символов
отличается от алфавитного среднего (чем больше связей / запрещенных
состояний), тем меньше число степеней свободы системы и тем выше возможная
компрессия.



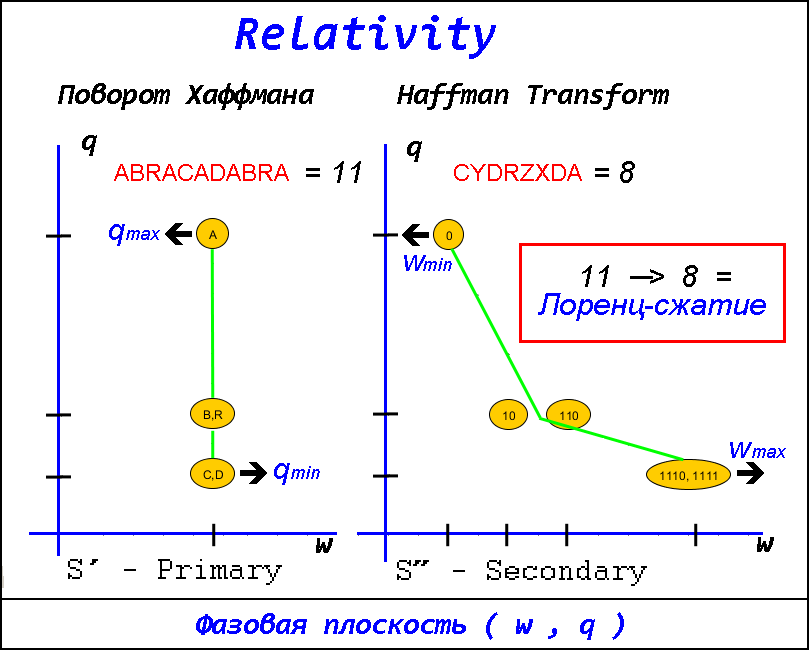Сравнивая исходное сообщение 'ABRACADABRA' с его сжатым вариантом 'CYDRZXDA'
в нашем трехбитовом алфавите, мы видим, что исходное сообщение никогда не не
использует три символа полного алфавита: 'X', 'Y', и 'Z'. Такие никогда не
используемые состояния будем называть запрещенными. В естественных языках или
кодах с коррекцией ошибок они играют роль приграничных охранных зон:
появление в потоке символа их запрещенного списка означает ошибку.

С точки зрения помехоустойчивости передачи, компрессия - это грязный трюк,
лишающий сообщение всякой возможности автокоррекции. В большинстве
практических применений, подобная цена оказывается неприемлемой и запрещенные
состояния приходится вводить в сжатое сообщение искусственно, применяя
различные схемы коррекции ошибок - от проверок четности до кодов
Рида-Соломона.

Подчеркну еще раз - число степеней свободы (число независимых координат
полного коодинатного пространства) при сжатии НЕ изменяется.

Наблюдаемое сокращение размера сообщения, по сути, "оптическая иллюзия",
возникающая вследствие перераспределения полного числа степеней свободы на
место ранее не использовавшихся запрещенных состояний.

Очевидно, что если сообщение изначально не содержало запрещенных состояний,
то оно не может быть сжато ("Энтропийный предел").

На практике, определение числа степеней свободы сообщения не является простой 
задачей.

Например, сообщение может содержать в равном количестве все символы алфавита, 
но их парные комбинации (дифтонги) различаются по кратности. Тогда уже следует 
говорить о запрещенных состояниях более высокого порядка. То же верно в отношении
трифтонгов итд.



Рассматривая сообщение как геометрический объект, а компрессию - как
сжимающее отображение, можно задаться вопросом о неподвижной точке этого
отображения.

Ранее предполагалась независимость координат, описывающих сообщение и, как
следствие, инвариантность размерности координатного пространства, но можно ли
быть уверенным в ортогональности координат исходного сообщения?
Неравномерность в распределении кратностей букв как будто свидетельствует об
обратном. Очевидно, что минимальная размерность координатного пространства
(минимум мощности) должна соответствовать максимальной симметрии сообщения.

Каждый алфавитный символ, встречающийся в сообщении, может быть описан двумя
наблюдаемыми координатами - его кратностью q и его битовой шириной w.

Назовем произведение p = q * w парциальной мощностью кодового символа.

Тогда полный битовый размер сообщения, очевидно будет равен сумме всех
парциальных мощностей, то есть произведению кратностей символов на их битовую
ширину:



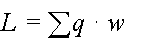Предельныму сжатию будет отвечать преобразование, минимизирующее этот
функционал.

Параметры q и w входят в выражение равноправно, но, на практике,
затруднительно независимо управлять кратностью символов, так как это влечет
изменение алфавита. В техниках сжатия такому изменению, обычно, отвечает
конструирование супербукв (например, RLE), а в техниках шифрования -
использование номенклаторов и омофонов.

С другой стороны, управлять битовой шириной символа можно почти независимо и
кодовые системы Морзе или Шеннона-Фано основаны именно на этом.

Насколько мал может быть полный размер сообщения, зависит, в первую очередь,
от размера бита. Из физических соображений, этот размер, вероятно, не может
быть меньше постоянной Планка. С другой стороны, считая в относительных
единицах и полагая, что размер кода может выражаться и нецелым числом, легко
найти относительный минимум данного функционала (в условных единицах).

Положим, что q и w всегда вещественны и положительны (оставляя без рассмотрения
вопрос о реализуемости и физическом смысле комплексных кодов. Во всяком случае,
пока передача сообщения рассматривается как односторонний процесс, коды обязаны
быть вещественными).